Prismメモ
前回の続きで、今回はPrismについて調べたのでそれについて記す。(lensパッケージ バージョン4.7に基づく)
前回書いたように、PrismはTraversalの一種であり、全体データの中の0個もしくは1個の部分データに着目する。また、Prismは「部分データから全体データを復元することができる」という、Lensにはない特徴を持つ。(そのため、Prismでは「全体」と「部分」という言い方は不適切かもしれない)
>>> (Right "hoge") ^. _Right "hoge" >>> "hoge" ^. re _Right Right "hoge"
この、Prismの効果を「逆転」する関数であるreがどういう仕組みになっているか気になったので、lensのマニュアルやソースコードを読んだ。
Prismの型
Prismのデータ型は以下のようになっている。
type Prism s t a b = forall p f. (Choice p, Applicative f) => p a (f b) -> p s (f t)
ちなみにTraversalのデータ型はこうである。
type Traversal s t a b = forall f. Applicative f => (a -> f b) -> s -> f t
Traversalと比べると、Prismは関数(->)のかわりにChoiceという型クラスが使われていることが分かる。実際、型コンストラクタ(->)はChoiceのインスタンスであるため、PrismはTraversalとしても使えるようになっている。
では、Choiceとは何か?ChoiceはProfunctorを拡張した型クラスであり、まずProfunctorを理解する必要がある。
Profunctor
ProfunctorはData.Profunctorモジュールで定義されている型クラスである。
Profunctorはdimap関数を持つ。
class Profunctor p where dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
関数の型コンストラクタ(->)はProfunctorのインスタンスである。
instance Profunctor (->) where dimap ab cd bc = cd . bc . ab
関数をモチーフとして考えると、Profunctorとは「2つの値の関係性を示すなにか」と考えることができる。dimap関数とは、2つの関数abとcdによって、Profunctorの持つ「関係性」の左辺(定義域)と右辺(値域)を変換する操作であると言える。
ただし、このようなアナロジーはProfunctorのインスタンスとして関数(->)を考えた場合に成り立つものであり、他のインスタンスでは必ずしも成り立たない。
dimapは左辺領域と右辺領域を両方同時に変換するが、左辺のみ変換するlmapと右辺のみ変換するrmapもProfunctorに定義されている。これらはdimapから作ることができる。
ChoiceはProfunctorを拡張した型クラスであり、left'とright'という関数を持つ。
class Profunctor p => Choice p where left' :: p a b -> p (Either a c) (Either b c) right' :: p a b -> p (Either c a) (Either c b) instance Choice (->) where left' ab (Left a) = Left (ab a) left' _ (Right c) = Right c right' = fmap
left'およびright'はProfunctorのEither型への自然な拡張である。これらはProfunctorの持つ「値の関係」をEither型のLeftもしくはRightにそれぞれ移す。移されなかった側は単にid関数で写像される。
prismコンストラクタ
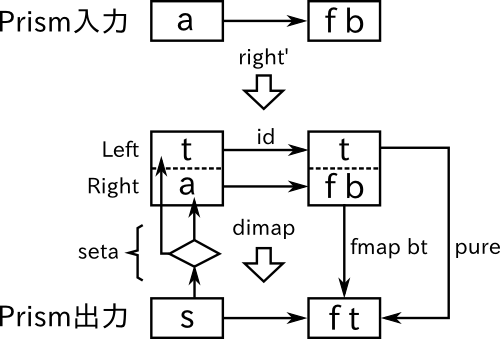
以上を踏まえ、Prismを作るコンストラクタ関数を見てみる。
prism :: (b -> t) -> (s -> Either t a) -> Prism s t a b prism bt seta = dimap seta (either pure (fmap bt)) . right'
prism関数は二つの関数を素材としてPrismを作る。
bt :: (b -> t)-- 「部分」から「全体」を作る関数seta :: (s -> Either t a)-- 「全体」から「部分」を取り出す関数(戻り値がRightの場合)。「部分」を取り出せなかった場合は「全体」をそのまま返す(戻り値がLeftの場合)。
こうしてできるPrismの動作は以下のようになる。
Prismへの入力データの型はp a (f b)である。まず、right'関数によってこれがp (Either c a) (Either c (f b))型へ変換される。
その後、dimapによってp (Either c a) (Either c (f b))の左辺領域と右辺領域が変換され、p s (f t)となる。型推論により、型変数cはtとなる。
prism関数では、bt(部分→全体)とseta(全体→部分)を与えることで、right'とdimapを使ってPrismを定義している。そのため、Prismは(->)以外のChoiceインスタンスに対しても適用することができる。
re関数
Prismの効果を逆転するre関数はこのように定義されている。
re :: AReview t b -> Getter b t re p = to (runIdentity #. unTagged #. p .# Tagged .# Identity)
to関数は通常の関数をLens化する関数であり、ここでは大した意味を持たない。重要なのはその引数であるカッコの中身である。
まず、見慣れない演算子(#.)と(.#)があるが、これはProfunctor型クラスのメソッドであり、そのデフォルト実装は以下のようになっている。
infixr 9 #. ( #. ) :: (b -> c) -> p a b -> p a c ( #. ) = \f -> \p -> p `seq` rmap f p infixl 8 .# ( .# ) :: p b c -> (a -> b) -> p a c ( .# ) = \p -> p `seq` \f -> lmap f p
ざっくり言って、rmapとlmapの演算子バージョンということっぽいが、ドキュメントにはいろいろ不穏な文言が書かれているので、左辺(または右辺)領域の「単純な」型変換にのみ使うべきものなようだ。
また、TaggedとunTaggedはTagged型に関する関数である。
newtype Tagged s b = Tagged { unTagged :: b } retag :: Tagged s b -> Tagged t b retag = Tagged . unTagged instance Functor (Tagged s) where fmap f (Tagged x) = Tagged (f x) instance Profunctor Tagged where dimap _ f (Tagged s) = Tagged (f s) lmap _ = retag rmap = fmap ( #. ) _ = unsafeCoerce Tagged s .# _ = Tagged s instance Choice Tagged where left' (Tagged b) = Tagged (Left b) right' (Tagged b) = Tagged (Right b)
Tagged型コンストラクタは2つの型引数を持つProfunctorであるが、実際にデータとして保持するのは右辺領域(b型)のデータのみである。そのため、rmapでは呼び出し元が与えたマップ関数fがきちんと適用されるが、lmapでは与えられたマップ関数は豪快に無視される。
このへんの動作は前回紹介したConstantファンクターに似ている。Constantファンクターは第1型引数のデータを保持し、第2型引数はフェイクであった。一方、Taggedは第1型引数がフェイクで第2型引数のデータを持つ。
以上を前提に、改めてre関数のカッコの中身を見る。演算子の優先順位を解決すると、以下のようになる。
(((runIdentity #. (unTagged #. p)) .# Tagged) .# Identity)
この演算のそれぞれの段階で型がどう変換されるかを見ていく。まず、引数pの型はAReview t bであり、これは展開すると、
AReview t b = Optic' Tagged Identity t b = Tagged b (Identity b) -> Tagged t (Identity t)
となる。
これを起点として型を変換していく。
p0 = p :: Tagged b (Identity b) -> Tagged t (Identity t) p1 = unTagged #. p0 :: Tagged b (Identity b) -> Identity t p2 = runIdentity #. p1 :: Tagged b (Identity b) -> t p3 = p2 .# Tagged :: Identity b -> t p4 = p3 .# Identity :: b -> t
ここで注意したいのは、この一連の操作で(#.)と(.#)が作用しているのはTagged Profunctorではなく、(->) Profunctorである点である。これらは単に関数の定義域と値域から2つのnewtypeを引き剥がしている。その結果、「部分」から「全体」を作る関数(b -> t)を得る。
なぜ(b -> t)を取ってくることができるかというと、Taggedが右辺領域の値しか持たないからだろう。Taggedを適用した場合のPrismの型は以下のようになる。
Tagged a (f b) -> Tagged s (f t)
Taggedは右辺領域の値しか持たないnewtypeなので、実質的にこれは
f b -> f t
と同じである。あとはfとして同様に単純なファンクターであるIdentityを使えば(b -> t)を取り出せる。
Iso
Prismはreで効果を逆転できるが、その結果はPrismではない。したがって、re (re p)はエラーとなる。
一方、再逆転可能なものとして、Isoというデータ型が定義されている。
- Control.Lens.Iso http://hackage.haskell.org/package/lens/docs/Control-Lens-Iso.html
IsoはLensとPrismの両方の性質を持つ。すなわち、
- 与えられた「全体」のうち、必ず1つの「部分」に着目する
- 「部分」から「全体」を構築できる
やはり「全体」と「部分」という言い方はここでは不適切であり、Isoは「本質的に同じデータの相互変換」を表すようだ。例えばByteStringとTextの相互変換などがIsoで表現される。
Isoのデータ型はこのようになっている。
type Iso s t a b = forall p f. (Profunctor p, Functor f) => p a (f b) -> p s (f t)
Prismと比べると、pはChoiceではなくProfunctorに、fはApplicativeではなくFunctorになっている。
Isoは「全体→部分」の正変換と「部分→全体」の逆変換を保持する。withIso関数を使うとそれらを取り出すことができる。
withIso :: AnIso s t a b -> ((s -> a) -> (b -> t) -> r) -> r
withIso関数の第2引数として与えられる関数に、正変換(s -> a)と逆変換(b -> t)が渡される。
withIso関数はExchangeというProfunctorを使うことで、Isoから正変換と逆変換を分離して取り出しているようだ。
Isoの効果を逆転する関数はfromである。
from :: AnIso s t a b -> Iso b a t s
fromの結果はIsoであり、from (from l) = lとなる。